Categories

• All categories (10)
• Blog (2)
• Derivatives (2)
• Markets (3)
• Structured Products (3)

Options traders... the last of the perma-bears?

So, we know (e.g. see here and previous blog post) that the implied probabilities from the prices of options are, in general, more bearish than realised frequencies. We also know how to compute those probabilities easily from market prices (if a bit rusty, give us a shout). 

For example, you can "bet" in the option markets that an index (say, the eurostoxx) will be higher or lower than 50% of today's level  in 5 year's time, and the market will, very often, give you odds (implied probability) of say ~20% of it being lower. You can do that in various way, from simple combinations of exchange traded options, to exotic options and structured products.

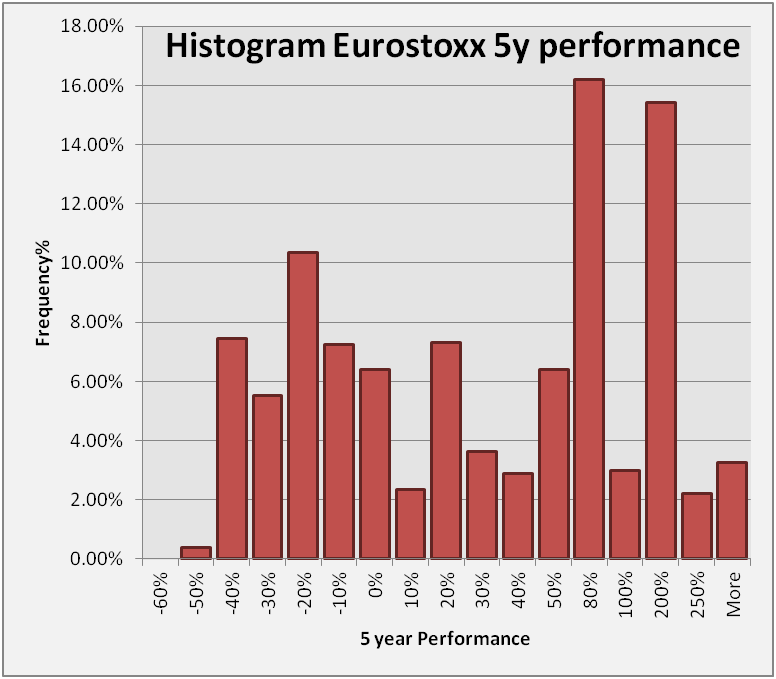
On the other hand, we also know that the "realised frequency" of such an event is much lower (see left, quick and dirty processing of data from Yahoo finance):

looking at all the 5yrs periods in the history of the eurostoxx prices you get ~0.4% (naively), and 8% for a ~40% drop, and it never dropped more than 60% (by the way: note how non-gaussian it is...).

So (naively...), if every day for the last several years you had put on a 5-year-long trade betting on the eurostoxx being higher than 50% at expiry, you would have always won - and quite strongly too. 

So are option prices wrong? Are options traders consistently losing money? Are they a bunch of wild eyed perma-bears?

The short answer is no - and I was going to write "of course, or there wouldn't be any option markets left", but that could be debated (as there are, allegedly, business sectors that go on for decades making losses).

But the long answer is "it depends"... what does "wrong price" mean? 

They play a different game

The key consideration (naively...) is that most price-makers for options (i.e. market-making firms and sell-side derivative-trading departments) are "dynamically hedging".

When they sell (or buy) an option, they do not price it thinking about the chances of the underlying being above or below the strike at expiry. Instead, they try to replicate the payoff of that option by buying and selling the underlying continuously (aka "dynamic delta hedging"). The cost of that replication strategy is the price of the option, and they think they know how to calculate it a priori (e.g. Black Scholes, or evolutions of it).

If their strategy works, then they will not lose money by taking the other side of your bet: they are playing a different game.  

Do their formulas, their replication strategies, work? Let's discuss another time... the point here is that that is their bet: - first order, it is a bet on the volatility of the underlying, i.e. how much it moves (in reality things get just a tad more complex than that...).

So the "right price" for them comes from the cost of their replicating strategy. While the "right price" for investors trading options or structured products WITHOUT dynamic hedging come from their subjective views on the future of the market. So they can both win (or lose, of course) - where winning is defined as making money by the end of the trade (crucially, you need to get to the end, avoiding bankruptcy by margin calls before - see below).

That's all very well, but where are the arbitrageurs?

One could still argue though that if enough investors took the downside bet, they would drive option prices down and hence the implied probabilities, until they got closer to realised frequencies.

Why doesn't it happen? 

First of all, there are such investors. Some of them have done very well out of it: Warren Buffet is a famous example, and some structured product investors are another one. Others less so: Victor Niederhoffer comes to mind, having blown up twice selling puts, but many hedge funds strategies boil down to something similar (or worse).

Two important differences between the winners and the losers come to mind: leverage (i.e. trade-sizing), and margin calls.

Buffet did sell his puts, but only on the condition of not posting collateral (there would be much more to say here).

The autocall investor never faces margin calls either: all the notional is at risk, but (hopefully)that does not represent all of his capital. One could say that Niederhoffer got the trade-sizing wrong - a minor detail :-)

There are not many investors/hedge funds now with the ability to commit capital to derivatives for a few years, without worrying about margin calls. On the other hand, there is constant demand of downside protection by long-term, long-only buy-side investors, thus keeping those implied probabilities high. This supply/demand imbalance has a role in keeping the implied probabilities higher than realised frequencies

But there are many more factors at play: for example, the non-normal distribution of frequencies and the risk-appetite or "utility function" of the investors all play a role.

Time to stop here, with one final note: it would appear that the scarcity of arbitrageurs is creating other interesting opportunities in long term derivatives, possibly even less risky than the simple one above.

Leave a comment

Boxes with an asterisk * next to them are required items

Name *
Email *	(Your email will not be published)
Website
Comment *
Enter the security code into the box below *